Dear Aagaard,
I’m developing a simulation to model the evolution of pore pressure following an earthquake using pylith 4.1.3. From my understanding, the pore pressure example in PyLith only allows the input of initial displacement conditions. As a result, the actual earthquake process is not included in the simulation.
To incorporate co-seismic deformation into the post-seismic diffusion process, I modified the example magma-2d as a base. I first ensured that step01_inflation runs correctly under a typical model.
However, when I changed the solution from:
solution = pylith.problems.SolnDispPresTracStrain
to:
solution = pylith.problems.SolnDispPresTracStrainLagrange
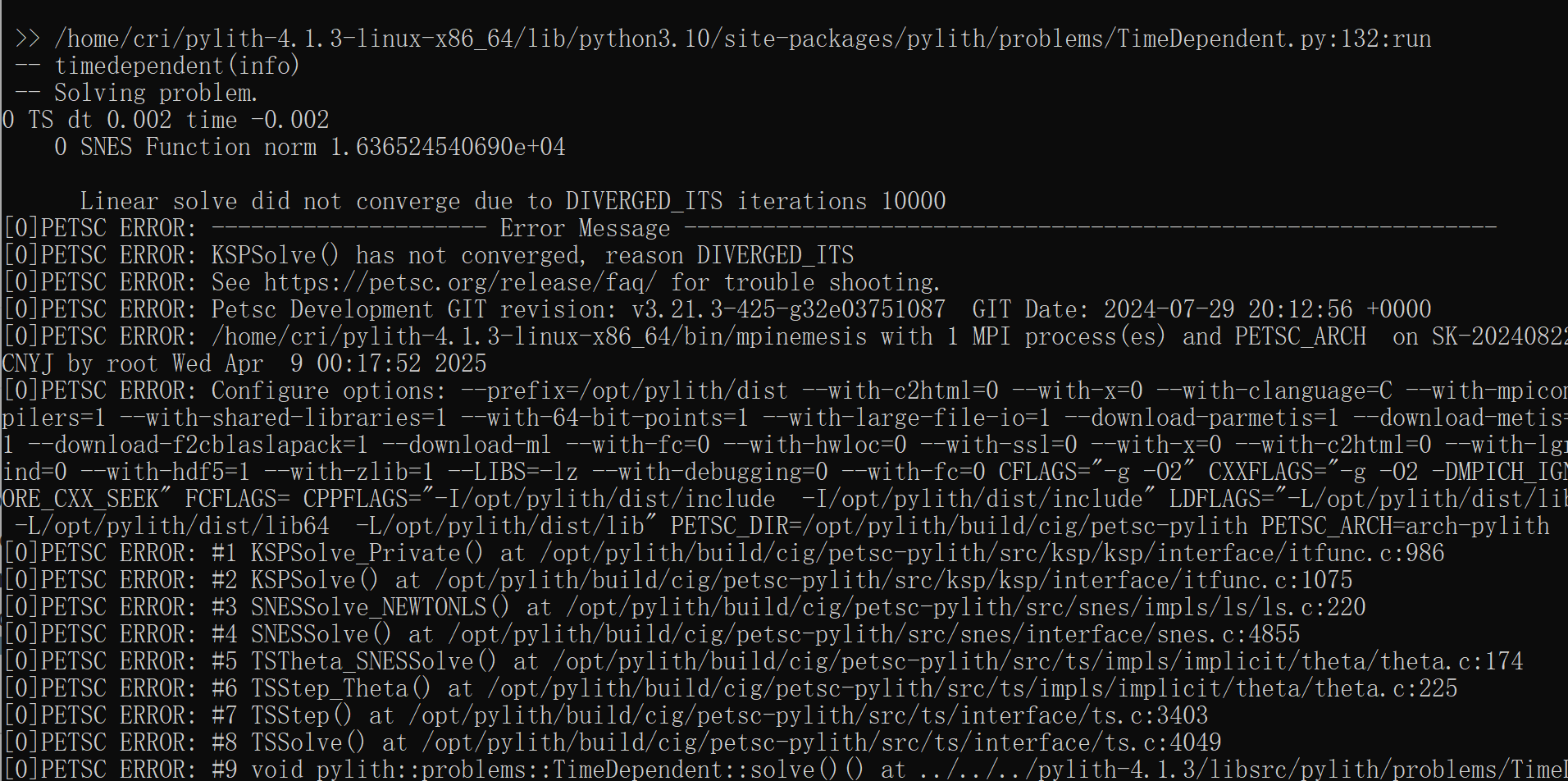
the simulation begin fails. If I only change the solution (without adding a fault to the model) and run pressure diffusion, the simulation fails to converge and eventually stops at the maximum number of iterations ( Figure 1).
If I then follow the coseismic example and add a fault, the simulation crashes immediately with a zero pivot error during LU factorization (Figure 2). I’m unable to locate the cause of the singular matrix or identify which part of the setup is responsible.
Am I on the right track by trying to use SolnDispPresTracStrainLagrange and add a fault in order to combine coseismic slip with postseismic pore pressure simulation? Is this the proper method?
If the information I provided is not sufficient to diagnose the problem, I would be happy to provide more details or files. I would greatly appreciate any advice or suggestions.
Best regards,
If you want to combine poroelasticity with a fault, then you are correct in using the SolnDispPresTracStrainLagrange solution field container. Some things to note:
- The solver will fail if you have the Lagrange multiplier field in the solution but do not have a fault. I will create a GitHub issue to note that this causes the solver to fail, so that we can generate an informative error message.
- I don’t think we have an example or test that uses poroelasticity with a fault. Robert Walker and Matt Knepley created an example for a paper in GJI based on strikeslip-2d. However, we have changed some solver defaults since then, so the settings they use may not be appropriate.
I think the following combination of the elasticity+fault solver settings and poroelasticity solver settings should work (but we haven’t tested these yet):
[pylithapp.problem.petsc_defaults]
# Turn off default solver settings
solver = False
[pylithapp.petsc]
# These two settings reorder the degrees of freedom so that we can use the variable point block Jacobi preconditioner
dm_reorder_section = True
dm_reorder_section_type = cohesive
# These are the poroelasticity solver settings
pc_type = fieldsplit
pc_fieldsplit_type = multiplicative
pc_fieldsplit_0_fields = 2
pc_fieldsplit_1_fields = 1
pc_fieldsplit_2_fields = 0
fieldsplit_trace_strain_pc_type = bjacobi
fieldsplit_pressure_pc_type = bjacobi
# These are the elasticity+fault solver settings
fieldsplit_displacement_pc_type = gamg
fieldsplit_displacement_ksp_type = gmres
mg_fine_pc_type = vpbjacobi
We will try to find time to set up appropriate automated tests and an example for poroelasticity with a fault in the next few weeks.
Dear aagaard,
Thank you for your prompt reply. I have tried the PETSc solver configuration you suggested, but it doesn’t seem to resolve the issue. I am currently working in the field for a while, but I will make time to further adjust the solver configuration. I will post an update in the forum once I make progress.
Thanks again for your assistance!
Best regards,
Dear Aagaard,
I’ve returned from fieldwork and completed the coupled modeling some time ago, but I’ve been held up in responding because one issue has been bothering me.
First, regarding the error in the program: as I posted in my earlier message with screenshots, the issue seems to stem from the fieldsplit configuration. I was able to run the simulation successfully with the following minimal settings, but I’m not sure whether using the default PETSc solver and preconditioner affects performance. When I slightly refined the mesh of my 3D model, the computation stopped due to failure to converge within 10,000 iterations.
[pylithapp.problem.petsc_defaults]
# Turn off default solver settings
solver = False
[pylithapp.petsc]
# These two settings reorder the degrees of freedom so that we can use the variable point block Jacobi preconditioner
dm_reorder_section = True
dm_reorder_section_type = cohesive
What’s been puzzling me more, though, is the behavior of the pressure field after fault rupture. As shown in the attached figure, negative pressure values appear near the fault tips. I initially assumed that, like mass, pressure should be greater than or equal to zero, and so I thought there might be something wrong with the parameters passed to the pressure field when handling the fault.
However, I’ve started to revise my understanding. Since the fault rupture itself is not a physical source of pressure, the pressure field should remain a conservative field. This would mean that the pressure values do not represent absolute values but rather changes or perturbations, which would explain why negative values can occur.
Am I correct in this line of reasoning?
Best regards,
I don’t know what you mean when you say
I was able to run the simulation successfully with the following minimal settings, but I’m not sure whether using the default PETSc solver and preconditioner affects performance. When I slightly refined the mesh of my 3D model, the computation stopped due to failure to converge within 10,000 iterations.
Removing the field split solver settings will very likely lead to poor convergence, if the solver converges at all. In some cases, the precondition may be just good enough that the solver will converge for a small problem but not for a larger problem. The recommended solver settings I provided above are based on the physics and have worked well for other users.
In the poroelasticity formulation, the fluid pressure is not “pressure change”. That said, the results you get will depend on your initial conditions. If your initial conditions use a very low fluid pressure, then it could become negative. You should also be careful about the ends of the faults. For example, uniform slip will generate very large stresses at the ends of the fault. A more realistic case would taper the slip near the ends of the fault.
Dear Aagaard,
It has been a while since I last left a message in the post. I’ve made some progress and gained a better understanding on most of the issues we previously discussed. I apologize for not updating my progress sooner, and I sincerely appreciate your responses and guidance.
The earthquake rupture model I’m using is based on a distributed slip model constrained by InSAR data. I applied spatial interpolation to assign non-uniform slip values across the fault. Specifically, I modeled the January 7, 2025, MW6.8 Shigatse earthquake in Tibet. So far, I’m very satisfied with the accuracy of the surface co-seismic deformation results. The introduction of pore pressure coupling has also yielded stable results, which reasonably reproduce the observed event.
I currently have one unresolved issue regarding the field split solver configuration. I’ve globally set the preconditioner to GAMG and the solver to GMRES, but for high-resolution mesh models, the solution fails to converge. I understand that fully coupled solves may not be appropriate for large-scale models. However, as I mentioned earlier, the field split configuration you suggested leads to a PETSc error: “Fields must be sorted when creating split.” I’ve tested it multiple times — the configuration works correctly when using solution = pylith.problems.SolnDispPresTracStrain, but results in the above error when using solution = pylith.problems.SolnDispPresTracStrainLagrange.
At the moment, I’m still trying to better understand the interface between PyLith problems and PETSc, and I’m continuing to work on this issue. I’ll provide further updates once I make progress.
Best regards,
It is difficult to follow your description of which solver settings you are using. The solver is complex with multiple layers.
These settings should scale well to large problem sizes. If the solution fails to converge, then add the following setting and capture the output to a log file and send it along with a description of the boundary value problem. This will help us diagnose solver issues.
[pylithapp.petsc]
ksp_monitor_true_residual = true
snes_view = true
These are the recommended solver settings for poroelasticity with a fault:
[pylithapp.problem.petsc_defaults]
# Turn off default solver settings
solver = False
[pylithapp.petsc]
# These are the poroelasticity solver settings
pc_type = fieldsplit
pc_fieldsplit_type = multiplicative
pc_fieldsplit_0_fields = 2
pc_fieldsplit_1_fields = 1
pc_fieldsplit_2_fields = 0
fieldsplit_trace_strain_pc_type = bjacobi
fieldsplit_pressure_pc_type = bjacobi
# These are the elasticity+fault solver settings
# These two settings reorder the degrees of freedom, so that we can use the variable point block Jacobi precondition.
# These are REQUIRED when using the variable point jacobi precondition, which we strongly recommend.
dm_reorder_section = True
dm_reorder_section_type = cohesive
fieldsplit_displacement_pc_type = gamg
fieldsplit_displacement_ksp_type = gmres
mg_fine_pc_type = vpbjacobi
Dear Aagaard,
I’ve tried the field split solver configuration you provided, but I’m still encountering the same error. I suspect I may not be explaining the underlying issue clearly enough, so I’m sharing the input scripts I used for the simulation. The two mesh models correspond to different resolutions.
poro.zip (5.1 MB)
[0]PETSC ERROR: Fields must be sorted when creating split
I can replicate the error. We will work on fixing the solver settings next week at the PyLith hackathon.
We have fixed the solver specification issues for poroelasticity with a fault in PyLith v4.2.1.