Questions Regarding Free Surface and Tractions in Spherical Shell Models

ASPECT
1

Dear all

I am conducting research that requires the use of a free surface in spherical shell geometry within ASPECT. During my simulations, I have noticed some unusual behavior in the surface traction results which I would like to bring to your attention and discuss.

I started by testing the free surface implementation in the 3D box model, specifically using the benchmark case from
free_surface_VE_cylinder_3D_loading.prm.
This model has a free surface on the top boundary with a traction load applied only on a quarter-circle loading region in the top corners. The traction magnitude is approximately t = \rho g h = 900 \times 9.8 \times 1000 \approx 8.82 \times 10^{6} \text{Pa} .

set Prescribed traction boundary indicators = top z: function

The rest of the boundaries are free-slip, set as:

set Tangential velocity boundary indicators = bottom, left, right, front, back

according to the standard free-slip conditions described in the ASPECT forum discussion on Free-slip boundary conditions.

In this Cartesian 3D box case, I verified the surface traction (t_i = \sigma_{ij} n_j ) behaves as expected:

  • On the free surface (top), tractions are zero(t_x=t_y=t_z=0) except in the loaded region where the applied traction(t_z) matches the theoretical estimate.
  • On the free-slip sides, the normal and tangential traction components correspond correctly with the expected zero tangential stresses and zero normal velocity.

I confirmed this by computing the traction vector in ParaView using the surface normal vectors and stress tensor data.

traction-x-step0-left_right
traction-x-step0-left_right1920×834 61.3 KB

traction-y-step0-front_back
traction-y-step0-front_back1920×834 83.7 KB

traction-z-step0-top_bottom
traction-z-step0-top_bottom1920×834 47.9 KB

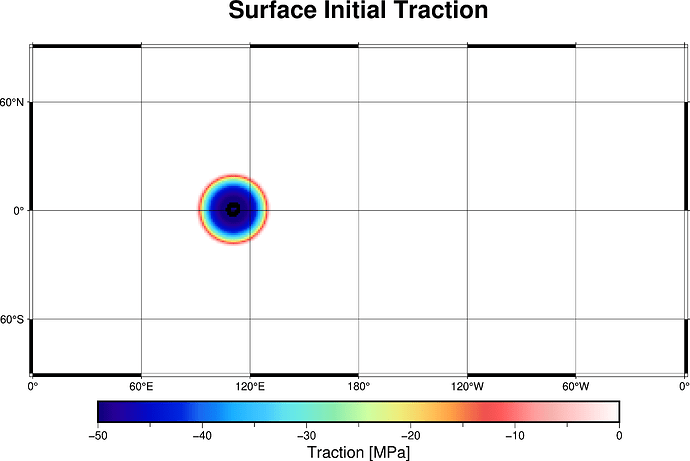
I then applied a similar procedure to a spherical shell model using a slightly modified
shell_simple_3d.prm

Using the same method in ParaView to compute the traction vector on the free surface, I found that the traction is not zero on the free surface where I expect it to be free of stress (except applied loads). This contradicts the usual free surface condition.

traction-x-step0
traction-x-step01920×828 102 KB

traction-y-step0
traction-y-step01920×828 102 KB

traction-z-step0
traction-z-step01920×828 102 KB

I am unsure whether this behavior indicates:

  • An issue with how the free surface boundary conditions or traction boundary conditions are transformed and applied in spherical or non-Cartesian coordinates,
  • Or if I have misunderstood some aspect of the theory or implementation. Do I need to convert from Cartesian coordinates to spherical coordinates before calculating the traction? I was under the impression that this was irrelevant.

I also tried the zero traction model and the result was the same.

This may be related to the previously opened issue Boundary traction on spherical geometries with free surface #4365, which remains unresolved.

  1. Is there an established benchmark for free surface in spherical geometry within ASPECT or in the literature?
    I searched for classical references but did not find a standard spherical free surface benchmark to validate this behavior. Any pointers or experience from the community would be very helpful.

  2. Regarding the ‘sticky air’ method benchmark from
    Geophysical Journal International paper by Crameri et al. (2012), whose ASPECT benchmark repository is at
    crameri_et_al,
    I noticed there is no explicit sticky air test case. I wonder:

    • Can sticky air be implemented reliably in spherical shell or chunk models?
    • Given sticky air usually requires high resolution and very low viscosity air layers, would this cause significant solver difficulties with shell-3d models?

shell_simple_3d-free_surface.prm (2.7 KB)
log.txt (13.5 KB)

Thank you very much for your attention and any insights.

Best,
Ninghui Tian