AMG vs. GMG Solver Inconsistency in 3D Elasticity Models in Spherical Domains

[tiannh7]

Hi all,

I am currently using the Aspect software to calculate 3D elasticity models in spherical domains, with a focus on viscosity and viscoelasticity. During my simulations, I’ve noticed some abnormal velocity results, and upon further investigation, I discovered that the AMG and GMG solvers provide inconsistent results, which I have discussed in this issue.

To troubleshoot this problem, I tested a simple example from the Aspect cookbook (shell_simple_3d.prm) to check whether the issue persists in other cases. When using a single material (without other components), the results from both solvers are consistent, whether in pure viscosity or viscoelasticity. However, when I apply a stratified material model (with a 60 km thick crust in the upper layer), the results from AMG and GMG become inconsistent.

This observation leads me to suspect that the inconsistency is related to the stratified material model, as the simpler, uniform material models do not exhibit this issue.

Additionally, I came across the following code snippet in the Aspect source code (aspect/source/material_model/rheology/elasticity.cc at main · geodynamics/aspect · GitHub), which might be relevant to understanding this issue:

// Functionality to average the additional RHS terms over the cell is not implemented.
// Also, there is no option implemented in this rheology module to project to Q1 the viscosity
// in the elastic force term for the RHS.
// Consequently, it is only possible to use elasticity with the Material averaging schemes
// 'none', 'harmonic average only viscosity', and 'geometric average only viscosity'.
// TODO: Find a way to include 'project to Q1 only viscosity'.
AssertThrow((this->get_parameters().material_averaging == MaterialModel::MaterialAveraging::none
             || this->get_parameters().material_averaging == MaterialModel::MaterialAveraging::harmonic_average_only_viscosity
             || this->get_parameters().material_averaging == MaterialModel::MaterialAveraging::geometric_average_only_viscosity
             || this->get_parameters().material_averaging == MaterialModel::MaterialAveraging::default_averaging),
            ExcMessage("Material models with elasticity can only be used with the material "
                       "averaging schemes 'none', 'harmonic average only viscosity' and "
                       "'geometric average only viscosity'. This parameter ('Material averaging') "
                       "is located within the 'Material model' subsection."));

This leads me to wonder whether the discrepancy could be due to how the averaging schemes are handled under the viscoelastic model. I’m not entirely clear on the details of the AMG and GMG solvers—could it be that their averaging schemes differ? Has anyone experienced a similar issue or might be able to offer any insights into this behavior?

Thank you in advance for any help or suggestions!

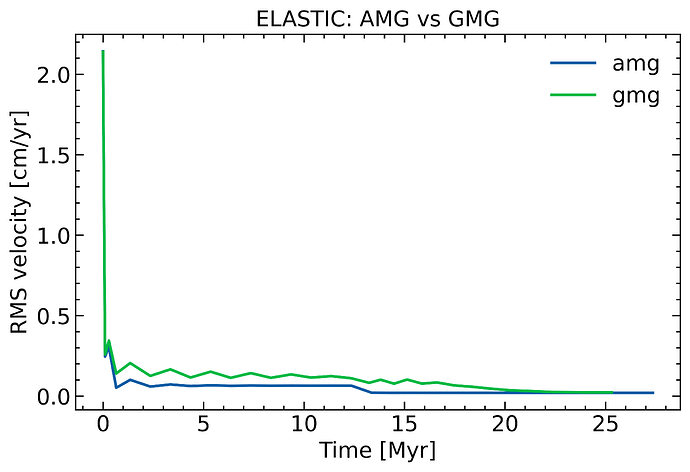
The RMS velocity, maximum velocity, and time step evolutions produced by the two solvers are as follows:
It seems that the AMG solver seems to be more stable and does not fluctuate.

The prm parameter files and logs related to the reproducible model are as follows:

amg-log.txt (34.5 KB)
gmg-log.txt (32.7 KB)
shell_simple_3d-amg-elastic-init_comp-fixed_dt-uniform.prm (1.3 KB)
shell_simple_3d-gmg-elastic-init_comp-fixed_dt-uniform.prm (1.3 KB)
shell_simple_3d.prm (2.0 KB)

Best regards,

Ninghui Tian

[jbnaliboff]

Hi @tiannh7,

Thanks for posting this very well laid out and throughout post! Likewise, apologies for not replying to the issue on github sooner.

I recall there being an issue with viscoelasticity in spherical models that was discovered by Maaike Weerdesteijn during her GIA benchmarks efforts, but is has been a while and I don’t recall the details.

With that said, the viscoelastic formulation has been undergoing a major revision (led by @anne-glerum) for quite sometime, and will hopefully be merged late this Spring or summer (final stages of testing now).

As a first step, can you try re-running your models using the new VEP implementation, which is located on this PR: Use correct stresses in visco-elasto-plastic rheology. I think it would be to confirm that the issue persists with the revised formulation, before moving onto other debugging.

To access this branch, you would do the following in your local aspect folder (assuming it was closed from github):

git remote add anne-glerum
git remote update
git checkout -b fix_stresses_elasticity anne-glerum/fix_stresses_elasticity

Note that using this branch will require modifying the input file structure a bit. There examples of how to do this on the PR, but let us know if some assistance would be helpful on this front.

Another quick thing to test using your current ASPECT build is the linear solver tolerance as follows:
subsection Solver parameters
subsection Stokes solver parameters
set Linear solver tolerance = 1e-8 # default is 1e-7
end
end

Do you see any key visual differences in the solution (velocity, pressure, viscoelastic stress) between the models with AMG and GMG for the stratified material case?

Cheers,
John

[tiannh7]

Hi @jbnaliboff,

Thank you so much for your kind and detailed reply! No worries at all about the delay in the GitHub issue response—I really appreciate your help here.

It’s great to hear that the viscoelastic formulation is undergoing a major revision, and I’m very glad to know that @anne-glerum is leading this important effort. I look forward to seeing it merged later this spring or summer!

Regarding your suggestions:

• I’ll definitely try running my models using the new fix_stresses_elasticity branch as you recommended. Thank you for providing the instructions to check out the branch. I may reach out again if I need assistance modifying the input file structure to match the new formulation.

• I also tested the linear solver tolerance setting with:

subsection Solver parameters
  subsection Stokes solver parameters
    set Linear solver tolerance = 1e-8
  end
end

This is easy to adjust, and I’ll keep an eye on any changes in solver behavior or stability.

As for your question about visual differences between AMG and GMG results in the stratified material case:

• At timestep = 0, both solvers (AMG and GMG) produce nearly identical results.
• However, at later time steps, I observe that the velocity field from GMG becomes significantly larger compared to AMG. This discrepancy seems to grow with time, suggesting a potential difference in how the two solvers handle the viscoelastic evolution in the layered structure.

Thanks again for your support and guidance—your suggestions are very helpful for narrowing down the issue. I’ll report back with results from the new VEP implementation.

Best regards,
Ninghui Tian

[jbnaliboff]

@tiannh7,

Thank you for the detailed responses, this is quite helpful.

A few follow up questions and suggestions:

1. Have you observed any similar behavior in 2D (spherical or cartesian) or 3D cartesian models with a layered rheology. This may be a quick path to debug if the issue is related to the spherical geometry or layered rheology in the current VE implementation within the main branch.
2. Are the velocity patterns at time step 0 (and the last time step for GMG) spatially correlated with the mesh geometry?

Cheers,
John

[tiannh7]

Dear John,

Thank you very much for your kind feedback and insightful suggestions.

1. Have you observed any similar behavior in 2D (spherical or cartesian) or 3D cartesian models with a layered rheology. This may be a quick path to debug if the issue is related to the spherical geometry or layered rheology in the current VE implementation within the main branch.

I believe the observed issue is likely not caused by the geometry itself, since the treatment of elastic stresses should be implemented consistently across different geometries. To further investigate this, I have tested the benchmark model viscoelastic_bending_beam.prm in 2D Cartesian geometry, and I did observe similar behavior there as well.

In particular, for the GMG solver configuration, I used the following setup:

include $ASPECT_SOURCE_DIR/benchmarks/viscoelastic_bending_beam/viscoelastic_bending_beam.prm

set Resume computation = false
set Output directory   = output-viscoelastic_bending_beam-layered-eta-gmg-harmonic

subsection Postprocess
  set List of postprocessors = basic statistics, composition statistics, temperature statistics, velocity statistics, visualization

  subsection Visualization
    set List of output variables            = material properties, strain rate, stress
    set Time between graphical output       = 10e3
    set Time steps between graphical output = 1
    set Interpolate output                  = true

    subsection Material properties
      set List of material properties = density, viscosity
    end
  end
end

subsection Termination criteria
  set End step             = 50
  set Termination criteria = end step
end

subsection Solver parameters
  subsection Stokes solver parameters
    set Stokes solver type      = block GMG
    set Linear solver tolerance = 1e-8
  end
end

subsection Material model
  set Model name = viscoelastic
  subsection Viscoelastic
    set Densities                   = 2800,  2800,  2800,  2800,  3300
    set Viscosities                 = 1.e18, 1.e18, 1.e18, 1.e18, 1.e24
    set Elastic shear moduli        = 1.e11, 1.e11, 1.e11, 1.e11, 1.e10
    set Fixed elastic time step     = 1e3
    set Use fixed elastic time step = false
    set Viscosity averaging scheme  = harmonic
  end
end

I also compared the behavior between AMG and GMG solvers:

< set Output directory   = output-viscoelastic_bending_beam-layered-eta-amg-harmonic
> set Output directory   = output-viscoelastic_bending_beam-layered-eta-gmg-harmonic

< set Stokes solver type      = block AMG
> set Stokes solver type      = block GMG

From my observations:

• The AMG solver appears to remain robust for viscoelastic configurations.
• In contrast, the GMG solver gradually becomes unstable over time.

I am currently preparing visual outputs to compare the results under different viscosity averaging schemes:

• Harmonic averaging
  

  
  
  
  
  
  
  

• Geometric averaging
  

  
  
  
  
  
  
  

• Maximum composition

Thanks again for your support and feedback!

Best regards,

Ninghui

[jbnaliboff]

Hi @tiannh7,

I believe the observed issue is likely not caused by the geometry itself, since the treatment of elastic stresses should be implemented consistently across different geometries.

Yes, in theory this should be the case. However, unexpected behavior can arise in some cases, as ASPECT is still approximating a spherical geometry within a cartesian reference frame.

To further investigate this, I have tested the benchmark model viscoelastic_bending_beam.prm in 2D Cartesian geometry, and I did observe similar behavior there as well.

We (the group working on new VEP formulation) have extensively tested the bending beam problem for a range of scenarios, and I don’t recall any divergence in the solution between AMG and GMG for that problem.

I suggest switching over testing on Anne’s branch going forward. Please let us know how it goes.

Cheers,
John

[tiannh7]

Hi John,

Thank you for your suggestion.

I have switched to Anne’s branch for testing as recommended. During the process, I encountered the following error:

An error occurred in line <196> of file </home/tiannh/aspect/Anne-Glerum/aspect/source/material_model/rheology/elasticity.cc> in function
void aspect::MaterialModel::Rheology::Elasticity<dim>::parse_parameters(dealii::ParameterHandler&) [with int dim = 2]
The violated condition was:
this->get_parameters().reaction_solver_type == Parameters<dim>::ReactionSolverType::fixed_step
Additional information:
If the operator splitting scheme is used, its solver should be set to
'fixed step'.

To address this, I added the following line to the .prm file based on the original benchmark input:

set Reaction solver type = fixed step

After making this change, the model was able to run. However, the issue of divergence between AMG and GMG solutions still remains. Specifically, I observed significant differences between the amg-main and amg-fix-stresses-elasticity branches even before 10 kyr.

Please let me know if there is anything else I should check or modify to further investigate this issue.

Best regards,

Ninghui

[jbnaliboff]

Hi @tiannh7,

Thank you for the update. If you don’t mind posting the PRM file for these models here, we (group working on VEP rheology) will discuss these results early next week.

I think Anne has made a number of updates to the bending beam benchmark, which is quite sensitive to how the initial composition is setup, particles versus composition, and averaging schemes.

Cheers,
John

[tiannh7]

Hi John,

Thank you very much for the feedback and for looking into this issue.

For this test, I used the PRM files from both the main branch and Anne’s branch:

• main branch version
• Anne’s branch version (fix_stresses_elasticity)

viscoelastic_bending_beam-anne-gmg.prm (6.8 KB)
viscoelastic_bending_beam-anne-amg.prm (6.8 KB)
viscoelastic_bending_beam-main-amg.prm (6.1 KB)

I made small modifications to the solver type and the viscosity averaging scheme, but otherwise kept the setup unchanged.

I really appreciate your attention to this and look forward to the discussion next week!

Best regards,
Ninghui

[jbnaliboff]

Excellent, thank you.

Cheers,
John

[tiannh7]

Hi John,

Great — I’m looking forward to any updates or insights you and the team might have as things progress.

Many thanks again for your attention to this issue and for all your help!

Best,
Ninghui

[anne-glerum]

Dear Ninghui,

Thank you for bringing this up. You are right in thinking that the GMG and AMG solvers use different averaging schemes by default. Note, however, that this refers to the material averaging, not the viscosity averaging. Material averaging averages the material model output over each element, while the viscosity averaging deals with how each composition contributes to the viscosity in a point.

If no material averaging scheme is specified, the AMG solver will by default not apply material averaging. The GMG solver will be default apply harmonic_average_only_viscosity or project_to_Q1_only_viscosity, depending on whether the problem includes elasticity and if the Newton solver is used.

This means that when the prm file doesn’t specify the material averaging method, two different problems are solved when switching from AMG to GMG. Although in the first prm files of the shell_simple_3D example, harmonic average only viscosity was set for material averaging, in your bending beam prms, I did not find that material averaging was set.

I’ve ran a few tests with my bending beam setup (which is indeed a bit modified) comparing GMG and AMG for geometric material averaging of the viscosity only. The prm file is attached. From the figures below, you can see that the AMG and GMG runs give the same results when using the same material averaging. It also shows that adding material averaging changes the problem (effective beam size) and there for the depth evolution of the beam changes. Could you try specifying the same material averaging in your tests and see if that still leads to differences between the two solvers for the bending beam? If not, we can focus on why the spherical setup showed a difference.

Cheers,
Anne

[tiannh7]

Dear Anne,

Thank you so much for your detailed explanation and for running additional tests — I really appreciate the time and effort you’ve put into this.

You are absolutely right — I had looked into material averaging schemes previously in the spherical setup, but at the time, the settings didn’t appear to have any noticeable effect. As a result, I neglected to re-apply or verify those settings in my bending beam tests — my apologies for overlooking that.

I’ll definitely try running the bending beam model again with explicitly specified material averaging to ensure consistency between the AMG and GMG solvers, as you suggested.

One small note — I may have missed it, but I couldn’t seem to find the .prm file you mentioned in your message. Would you mind reattaching it when you get a chance?

Thanks again for your kind help and close attention to this issue — it’s been incredibly helpful!

Best,
Ninghui

[anne-glerum]

Apologies, I forgot to attach the prm. Here it is.

Cheers,
Anne

RL9_viscoelastic_bending_beam_smooth25m_DGlimiter_Newton_GMG_dtc500_dte500_averaginggeometric_IGR1_IAR0.prm (7.3 KB)

[tiannh7]

Dear Anne,

Thank you very much again for sharing the .prm file and for your insightful explanation:)

Following your suggestion, I explicitly specified both Material averaging and the Viscosity averaging scheme in the following way:

subsection Material model
  set Material averaging = geometric average only viscosity
  set Model name = viscoelastic
  ...
    set Viscosity averaging scheme = geometric
  end
end

After reviewing your attached parameter file, I noticed that beyond changes in the number of viscoelastic stress fields (e.g., ve_stress_**_old), the most significant differences may lie in the nonlinear solver setup and mesh refinement strategy. The default main branch I had been using applies:

• Nonlinear solver scheme = single Advection, single Stokes
• Initial global refinement = 0

whereas your modified setup used:

• iterated Advection and Newton Stokes
• Initial global refinement = 1

To investigate this further, I ran a few tests varying these parameters:

• Increasing the mesh resolution appeared to smooth the RMS velocity curves and reduced their magnitude in both the main and fix_stresses_elasticity branches.
• When using iterated Advection and Stokes, the AMG solver (02-anne-fix-AMG-Igr1) remained stable, while the GMG solver (02-anne-fix-GMG-Igr1) showed oscillatory and unstable behavior.
• Switching to iterated Advection and Newton Stokes dramatically improved the agreement between AMG and GMG, with both producing consistent results.

These results lead me to two follow-up questions:

1. Is there an analytical or benchmark solution available that would help evaluate which setup (e.g., main vs fix_stresses_elasticity) more closely matches the expected solution?

I noticed that the study by Weerdesteijn et al., 2023 also used the single Advection, single Stokes scheme for viscoelastic modeling—so I wonder whether that choice remains valid for our bending beam benchmark.
2. Is there a way to tune parameters such that the GMG solver behaves more similarly across solver schemes (iterated Advection and Stokes vs iterated Advection and Newton Stokes)?
That is, are there specific settings (e.g., smoother type, preconditioners, tolerance values) that could stabilize GMG under the iterated Advection and Stokes scheme?

In the vertical axis label, I noticed the notation \tau^{0}_{cxx} — I just wanted to confirm: does this refer to the x-direction component of the deviatoric stress? And if so, is the unit in Pa? Also, for the second plot showing velocity — is the vertical axis unit in meters per year (m/yr) rather than meters per second (m/s)?

Thanks again for your time and support—it’s been incredibly helpful to walk through this comparison process based on your suggestions.

Best,
Ninghui

[jbnaliboff]

Hi @tiannh7 - A few initial responses until Anne has a chance to weigh in.

• Solver scheme - the new VEP branch requires using an iterated Advection scheme, but I imagine most of the setups with a linear viscoelastic rheology don’t require too many iterations to reduce the Stokes solution residual to the specified tolerance (Anne will be able to confirm).

• Setting Initial global refinement to a higher value (versus using more X/Y repetitions) should improve the linear solver convergence behavior.

• When using iterated Advection and Stokes, the AMG solver (02-anne-fix-AMG-Igr1) remained stable, while the GMG solver (02-anne-fix-GMG-Igr1) showed oscillatory and unstable behavior.
• Switching to iterated Advection and Newton Stokes dramatically improved the agreement between AMG and GMG, with both producing consistent results.

In theory one should be able to converge to the same solution for both nonlinear solver schemes. However, for iterated Advection and Stokes you may need to use a much higher linear solver tolerance to reach the specified nonlinear solver tolerance (or if it is too loose the nonlinear solution may not be robust). Some related discussion can be found here.

1. Is there an analytical or benchmark solution available that would help evaluate which setup (e.g., main vs fix_stresses_elasticity) more closely matches the expected solution?

You should definitely use fix_stresses_elasticity, which has been carefully tested against all of the viscoelastic and viscoelastoplastic benchmarks (and new ones) in the benchmarks folder.

For simple viscoelastic linear rheologies and models with small deformations, the two branches will show minimal divergence in most cases.

For larger finite deformation models and/or highly nonlinear material behavior, the solutions between the two branches will start to diverge.

I noticed that the study by Weerdesteijn et al., 2023 also used the single Advection, single Stokes scheme for viscoelastic modeling—so I wonder whether that choice remains valid for our bending beam benchmark.

The new branch requires using an iterated Advection scheme, but the results for that benchmark did not change significantly between the two branches (it is a small finite deformation model).

2. Is there a way to tune parameters such that the GMG solver behaves more similarly across solver schemes (iterated Advection and Stokes vs iterated Advection and Newton Stokes)?

See some of the discussion above, but happy to discuss test results as you work through the process of testing different linear/linear solver tolerances and nonlinear solver schemes (iterated Advection and Stokes versus iterated Advection and Newton Stokes, etc)

Cheers,
John

[tiannh7]

Hi @jbnaliboff ,
Thank you very much for the detailed explanations and suggestions!

In theory one should be able to converge to the same solution for both nonlinear solver schemes. However, for iterated Advection and Stokes you may need to use a much higher linear solver tolerance to reach the specified nonlinear solver tolerance (or if it is too loose the nonlinear solution may not be robust). Some related discussion can be found here.

I really appreciate the previous thorough viscoplastic test you shared. I found that using a high precision convergence criterion — setting iterated Advection and Stokes = 1e-7 and Linear solver tolerance = 1e-8 — yielded quite consistent results between the iterated Advection and Stokes and the iterated Advection and Newton Stokes schemes (as shown here).

However, in the case of the viscoelastic beam benchmark, applying similar settings (e.g., iterated Advection and Stokes = 1e-7 and Linear solver tolerance = 1e-8, or even tighter criteria like 1e-9) still leads to instability and does not exhibit the same level of convergence as the Newton approach.

I’ll continue testing with different solver tolerances and schemes, and I’m happy to share results for further discussion.

Thanks again for your help and guidance.

02-anne-fix-GMG-Igr1-NLtol1e-8_Ltol1e-9.prm (7.1 KB)

Best regards,
Ninghui

[anne-glerum]

Hi Ninghui,

Just to make sure I understand: when using AMG on the bending beam benchmark, iterated Stokes and iterated Newton Stokes give very similar results, but when using GMG they differ, even with very strict tolerances?

In the vertical axis label, I noticed the notation — I just wanted to confirm: does this refer to the x-direction component of the deviatoric stress? And if so, is the unit in Pa? Also, for the second plot showing velocity — is the vertical axis unit in meters per year (m/yr) rather than meters per second (m/s)?
Yes, well spotted. It’s m/yr and Pa.

Cheers,
Anne

[tiannh7]

Hi Anne,

Apologies — I may not have explained it clearly enough earlier, or perhaps some of the plot colors were difficult to distinguish.

What I meant is the following:

• For the Newton Stokes solver, AMG and GMG converge to consistent results, even without enforcing particularly strict tolerances.
• For the iterated Advection and Stokes nonlinear solver scheme:
  • The AMG solver remains stable, but its result still shows some differences compared to Newton.
  • The GMG solver, however, fails to converge to the same result — even when using tighter tolerances.

Thank you very much for your attention to this and for helping to clarify the differences. I really appreciate your help in working through these solver behaviors!

Best,
Ninghui

[tjhei]

Anne and John:

I apologize for jumping in and asking something tangentially related:
How useful would it be to allow GMG to not require viscosity averaging (for these kind of problems or in general?)? This could be implemented with a little bit of effort (but I don’t want to work on it if it turns out to not be very useful as it is likely slightly slower and requires a bit more memory).